
Students are fascinated by concrete examples of symmetry in nature and in art. The tool that he developed to understand symmetry, namely group theory, has been used by mathematicians ever since to define, study, and even create symmetry. Recognizing the symmetry that exists among the roots of an equation, Galois was able to solve a centuries-old problem. In the Elements, Euclid exploited symmetry from the very first proposition to make his proofs clear and straightforward. Symmetry is certainly one of the most powerful and pervasive concepts in mathematics. Symmetry is found everywhere in nature and is also one of the most prevalent themes in art, architecture, and design - in cultures all over the world and throughout human history. This paper will describe how I have been introducing students in a general education geometry course to the concept of symmetry in a way that I feel gives them a comprehensive understanding of the mathematical approach to symmetry.
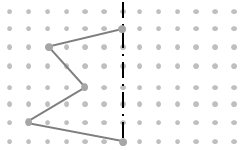
Reflection symmetry full#
Nevertheless, it is natural to want to teach these concepts in their full value from the very beginning. Students begin to use symmetry with commutativity and associativity in arithmetic, making more use of it in Euclidean geometry and plane geometry, and may eventually see it in terms of transformation groups. Students first see infinity appearing as the potential infinite inherent in the positional number system, then implicit in plane geometry, and eventually underlying all of calculus and analysis. Understanding these concepts and the tools for studying them is often a long process that extends over many years in a student’s career.

In mathematics, certain basic concepts, such as symmetry and infinity, are so pervasive and adaptable that they can become elusive to the student.
Symmetry - A Link Between Mathematics and Life


 0 kommentar(er)
0 kommentar(er)
